Shen Huang's Blog
0%

Posted on Edited on

题意：

每个物体都有一个权值a[i]，求出的是背包目前sum值不能再放入任何一个物体，意思就是sum+a[i] <= d这个的方案数

想法：

先排序,sum[i]，前i个物体的权值和

可以枚举1-N那个物体不在背包的，这样子i之前的全都在背包里，在i+1-N的进行背包，背包的大小在d-sum[i]到d-sum[i-1]+1之间，相想为何要+1

然后从N开始向下枚举，改一改如上算法就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/* From: Lich_Amnesia
 * Time: 2014-03-06 15:04:22
 *
 * POJ 3093 01背包
 * */ 
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl

#define maxn 1010
int dp[maxn],a[maxn];
int main(){
	int T,t = 0;
	int n,d,sum;
	cin >> T;
	while (t ++ < T){
		scanf("%d%d", &n, &d);
		sum = 0;
		for (int i = 1; i <= n; i ++){
			scanf("%d", &a[i]);
			sum += a[i];
		}
		sort(a + 1,a + n + 1);
		memset(dp,0,sizeof(dp));
		dp[0] = 1;
		int ans = 0;
		for (int i = n; i > 0; i --){
			sum -= a[i];
			for (int v = max(d - sum - a[i] + 1, 0); v <= d - sum; v++)
				ans += dp[v];
			for (int v = d; v >= a[i]; v --)
				dp[v] += dp[v - a[i]];
		}
		printf("%d %dn",t,a[1] > d ? 0 : ans);
	}
	return 0;
}

Posted on Edited on

简单递推，记得记录路径
dp[i][j] = max(dp[i-1][j-1] + a[i][j], dp[i][j-1])
可能会出现
3 5
-50 -50 -50 -50 -50
-50 -50 -50 -50 -50
-50 -50 -50 -50 -50
这样的数据
记得初始化好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
/* From: Lich_Amnesia
 * Time: 2014-03-05 21:53:31
 *
 * poj 1157 || sgu 104 简单递推
 * */
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl

#define maxn 110
int a[maxn][maxn];
int dp[maxn][maxn];
int pre[maxn][maxn];

int main(){
	int f,v;
	while (~scanf("%d%d", &f, &v)){
		memset(pre,0,sizeof(pre));
		memset(dp,0,sizeof(dp));
		for (int i = 1; i <= f; i ++){
			for (int j = 1; j <= v; j ++){
				scanf("%d", &a[i][j]);
			}
		}
		for (int i = 1; i <= f; i ++){
			dp[i][i] = dp[i-1][i-1] + a[i][i];
			pre[i][i] = 1;
		}
		for (int i = 1; i <= f; i ++){
			for (int j = i + 1; j <= v; j ++){
				dp[i][j] = dp[i][j-1];
				if (dp[i-1][j-1] + a[i][j] > dp[i][j]){
					dp[i][j] = dp[i-1][j-1] + a[i][j];
					pre[i][j] = 1;
				}
			}
		}
		printf("%dn",dp[f][v]);
		int ans[maxn],cnt = 0;
		for (int i = f,j = v; i > 0; --i){
			while (pre[i][j] == 0) j --;
			ans[cnt ++] = j --;
		}
		while (cnt --) printf("%d ",ans[cnt]);
		printf("n");
	}
	return 0;
}

Posted on Edited on

注意判定是逆时针旋转扫描边就行（这个还不是很清楚，check函数）

每次走的时候选择最左的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
/* From: Lich_Amnesia
 * Time: 2014-03-03 19:19:41
 *
 * zoj 1030 每次走时选离当前边最左的走
 * */
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl
#define maxn 300
const double PI = acos(-1.0);
const double EPS = 1e-10;
vector<pair<double,int> > g[maxn];

int k,T,d,u,v,Len,n;
int ans;double x[maxn],y[maxn];int mark[maxn][maxn];

bool check(double a,double b){
	if (b > a + EPS) return b + EPS < a + PI;
	else return b + EPS < a - PI;
}

void dfs(int u,int v){
	vector<pair<double,int> >::iterator it;
	for (it = g[v].begin(); it->second != u; it ++);
	double w = it->first;
	if (it == g[v].begin()) it = --g[v].end();
	else it --;

	if (mark[v][it->second] == -1){
		mark[v][it->second] = mark[u][v] + 1;
		dfs(v, it->second);
	}else {
		if (mark[v][it->second] != -2 &&
			mark[u][v] - mark[v][it->second] + 1 == Len &&
			check(it->first,w))
			ans ++;
	}
	mark[u][v] = -2;
}

int main(){
	cin >> T;
	while (T--){
		scanf("%d", &n);
		for (int i = 1; i <= n; i ++) g[i].clear();
		for (int i = 1; i <= n; i ++){
			scanf("%d", &u);
			scanf("%lf%lf", &x[u], &y[u]);
			scanf("%d", &d);
			for (int j = 0; j < d; j ++){
				scanf("%d", &v);
				g[u].pb(mp(0,v));
			}
		}
		vector<pair<double,int> >::iterator it;
		scanf("%d", &Len);
		for (int i = 1; i <= n; i ++){
			for (it = g[i].begin(); it != g[i].end(); it++){
				it->first = atan2(y[it->second] - y[i],x[it->second] - x[i]);
			}
			sort(g[i].begin(),g[i].end());
		}
		ans = 0;
		memset(mark, -1, sizeof(mark));
		for (int i = 1; i <= n; i ++){
			for (it = g[i].begin(); it != g[i].end(); it ++){
				if (mark[i][it->second] == -1){
					mark[i][it->second] = 0;
					dfs(i,it->second);
				}
			}
		}
		printf("%dn",ans);
	}
	return 0;
}

Posted on Edited on

题意：有n个人排成一列，给出前k个人的数字，从第k+1个人开始，给他们分配数字，分配的方法是取当前没有出现过的最小正整数，例如8人，前3人的数字为3 5 8，第4到第8个人的数字分别为1 2 4 6 7，整个序列为3 5 8 1 2 4 6 7

数据很大，不可能模拟

1.留意到一点，因为是取最小的没用过的正整数，所以我们可以先把所有可能用的正整数保存下来，按区间保存

2.例如已经用了3 5 8，没用的就是

[1,2] 2个

[4,4] 1个

[6,8] 3个

现在

要为第k+1个人分配数字，那么可以立刻知道是分配1，因为1是第1个没有用过的

要为第k+5个人分配数字，可以立刻知道是7，因为7是第5个没有用过的数字

所以要为第m个数字分配数字，在上面没有用过的数字表里面找，先找到它在哪一块，再找到是哪一块的第几个，其中找在哪一块，用二分即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
/* From: Lich_Amnesia
 * Time: 2014-03-03 16:51:26
 *
 * uva 12598 二分
 * */
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl

#define maxn 51010

int sum[maxn],num[maxn],use[maxn];

struct Segment{
	int l,r,len;
	Segment(){}
	Segment(int a,int b,int c){
		l = a;r = b; len = c;
	}
}seg[maxn];
int nm;
int binary(int key){
	int l = 1,r = nm -1,ans;
	while (l <= r){
		int mid = MID(l,r);
		if (key <= sum[mid]){
			ans = mid; r = mid - 1;
		}else l = mid + 1;
	}
	return ans;
}

int main(){
	int T,n,k,q;
	cin >> T;
	int t = 0;
	while (t ++ < T){
		scanf("%d%d%d", &n, &k, &q);
		for (int i = 1; i <= k; i ++){
			scanf("%d", &num[i]);
			use[i] = num[i];
		}
		use[0] = 0;use[k + 1] = INF;
		sort(use, use + k + 2);

		nm = 1;int r,l;
		seg[0] = Segment(0,0,0);
		for (int i = 1; i <= k + 1; i ++){
			l = use[i-1] + 1;
			r = use[i] - 1;
			if (r > n) r = n;
			if (r - l + 1 > 0) {
				seg[nm ++] = Segment(l,r,r - l + 1);
			}
		}

		memset(sum,0,sizeof(sum));
		sum[0] = 0;
		for (int i = 1; i < nm; i ++){
			sum[i] = seg[i].len + sum[i - 1];
		}

		printf("Case %d:n",t);
		int cnt;
		for (int i = 0; i < q; i ++){
			scanf("%d", &cnt);
			if (cnt <= k) {
				printf("%dn", num[cnt]);continue;
			}
			cnt -= k;
			int index = binary(cnt);
			printf("%dn",seg[index].r - (sum[index] - cnt));
		}
	}
	return 0;
}

Posted on Edited on

二分答案

假设当前二分的答案为 t，那么：

对于ai <= t的衣服，显然让它们自然风干就可以了。

对于ai > t的衣服，我们需要知道该衣服最少用多少次烘干机。

设该衣服用了x1分钟风干，用了x2分钟烘干机。

那么有 x1 + x2 = t 和 ai <= x1 + x2 * k，联立两式可得 x2 >= (ai - t) / (k - 1)，即最少使用次数为[(ai - t) / (k - 1)] 的最小上界。

最后，判断一下总使用次数是否少于 t 即可。

记得不要除零

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
/* From: Lich_Amnesia
 * Time: 2014-03-03 17:33:06
 *
 * POJ 3104 二分答案
 * */
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl

#define maxn 100050
typedef long long ll;
ll k,num[maxn],ans;
int n;

bool check(ll mid){
	ll cnt = 0;
	for (int i = 0; i < n; i ++){
		if (num[i] <= mid) continue; 
		cnt += (num[i] - mid + k - 2)/(k - 1);//加上k-2相当于取上界了
		//k-1可能会等于0啊
		if (cnt > mid) return false;
	}
	return true;
}

ll solve(){
	ll l = 1,mid, r = ans;
	while (l <= r){
		mid = MID(l,r);
		if (check(mid)) {
			r = mid - 1;
			ans = mid;
		}else l = mid + 1;
	}
	return ans;
}

int main(){
	scanf("%d", &n);
	ans = 0;
	for (int i = 0; i < n; i ++){
		scanf("%lld", &num[i]);
		ans = max(num[i],ans);
	}
	scanf("%lld", &k);
	printf("%lldn",k == 1?ans : solve());
	return 0;
}

Posted on Edited on

同2167，只不过这次不是单位圆覆盖了，是给定半径了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
/* From: Lich_Amnesia
 * Time: 2014-02-24 08:56:31
 *
 * ZOJ 2978
 * */
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl
#define maxn 2010
#define EPS 1e-8
typedef struct Point{
	double x,y;
	Point(double x = 0, double y = 0):x(x),y(y){}
}Vector;
int n;double R;
struct Circle{
	Point c;
	double r;
	Circle(Point c = Point(), double r = 0):c(c),r(r){}
};
struct Node{
	double angle;
	int id,flag;
}node[maxn];

bool cmp(Node a,Node b){
	return a.angle == b.angle ? a.flag > b.flag : a.angle < b.angle;
}

Vector operator + (Vector a, Vector b) {
	return Vector(a.x + b.x, a.y + b.y);
}
Vector operator - (Vector a, Vector b) {
	return Vector(a.x - b.x, a.y - b.y);
}
Vector operator * (Vector a, double k) {
	return Vector(a.x * k, a.y * k);
}

inline double cross(Vector a, Vector b) {
	return a.x * b.y - a.y * b.x;
}
inline double dis_pp(Point a,Point b){
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

Point intersection_ll(Point a, Vector i, Point b, Vector j) {
	Vector k = a - b;
	double t = cross(j, k) / cross(i, j);
	return a + i * t;
}

// 计算直线与圆的交点保证直线与圆有交点,
// 计算线段与圆的交点可用这个函数后判点是否在线段上
void intersection_cl(Circle c, Point p, Vector v, Point &p1 , Point &p2) {
	Point l1 = p, l2 = p + v;
	Vector u = Vector(-v.y, v.x);
	Point p0 = intersection_ll(p, v, c.c, u);
	double d1 = dis_pp(p0 , c.c);
	double d2 = dis_pp(l1 , l2);
	double t = sqrt(c.r * c.r - d1 * d1)/ d2;
	p1.x = p0.x + (l2.x - l1.x) * t;
	p1.y = p0.y + (l2.y - l1.y) * t;
	p2.x = p0.x - (l2.x - l1.x) * t;
	p2.y = p0.y - (l2.y - l1.y) * t;
}

// pre -req: 保证圆与圆有交点, 圆心不重合
void intersection_cc(Circle c1 , Circle c2 , Point& p1 , Point& p2){
	double d = dis_pp(c1.c, c2.c);
	double t = (1.0 + (c1.r * c1.r - c2.r * c2.r) / d / d) / 2;
	Point u = Point(c1.c.x + (c2.c.x - c1.c.x) * t, c1.c.y + (c2.c.y - c1.c.y) * t);
	Point v = Point(u.x + c1.c.y - c2.c.y, u.y - c1.c.x + c2.c.x);
	intersection_cl(c1 , u, v - u, p1 , p2);
}

Point p[maxn];

inline int solve(int n){
	int ret = 1,cnt = 0;
	bool vis[maxn];
	for (int i = 0; i < n; i ++){
		cnt = 0;
		for (int j = 0; j < n; j ++){
			if (i == j) continue;
			if (dis_pp(p[i], p[j]) > 2 * R + EPS) continue; //也许不需要开根
			Point a,b;
			intersection_cc(Circle(p[i],R), Circle(p[j],R), a, b);
			node[cnt].id = j;
			node[cnt].flag = -1;
			node[cnt ++].angle = atan2(a.y - p[i].y, a.x - p[i].x);

			node[cnt].id = j;
			node[cnt].flag = 1;
			node[cnt ++].angle = atan2(b.y - p[i].y, b.x - p[i].x);
		}

		if (cnt == 0) continue;

		sort(node, node + cnt, cmp);
		memset(vis,0,sizeof(vis));

		int s = 0,sum = 1,k = 0;//s表示弧的对数
		while (s < cnt / 2){
			if (node[k].flag > 0){
				sum ++;
				ret = max(ret,sum);
				vis[node[k].id] = 1; // 标记进入
			}else {
				if (vis[node[k].id]){//遇到出去的点，并且之前已经进去过，
									//那么走过了一个完整的弧，标记下
					s ++;
					sum --;
				}
			}
			k ++;//保持k在0 到cnt-1
			k %= cnt;

		}

	}
	return ret;
}

int main(){ 
	while (~scanf("%d%lf",&n,&R) && n){
		for (int i = 0; i < n; i ++){
			scanf("%lf%lf", &p[i].x, &p[i].y);
		}
		int ans = solve(n);

		printf("It is possible to cover %d points.n",ans );
	}
	return 0;
}

Posted on Edited on

先上一个O(n^3)的算法

也就是枚举两个距离小于2的点，用它们来固定一个圆，当然对称圆也要算，再枚举所有点，看是不是在这个圆内，当然这题这样就可以水过，不过这并不是最优的。

注意ans至少为1个.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

/* From: Lich_Amnesia
 * Time: 2014-02-24 08:56:31
 *
 * POJ 1981
 * */
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl
#define maxn 310
#define EPS 1e-8
typedef struct Point{
	double x,y;
	Point(double x = 0, double y = 0):x(x),y(y){}
}Vector;
int n;
struct Circle{
	Point c;
	double r;
	Circle(Point c = Point(), double r = 0):c(c),r(r){}
};

bool cmp(Point a,Point b){
	return a.x == b.x ? a.y < b.y : a.x < b.x;
}

Vector operator + (Vector a, Vector b) {
	return Vector(a.x + b.x, a.y + b.y);
}
Vector operator - (Vector a, Vector b) {
	return Vector(a.x - b.x, a.y - b.y);
}
Vector operator * (Vector a, double k) {
	return Vector(a.x * k, a.y * k);
}

inline double dis_pp(Point a,Point b){
	return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}

Point p[maxn];

inline int solve(Point a, Point b){
	Point mid = Point((a.x + b.x) / 2, (a.y + b.y) / 2);
	double angle = atan2(a.y - b.y, a.x - b.x) + acos(-1.0)/2;//圆直径的倾斜角
	double len = sqrt(1 - dis_pp(a,b)/ 4);
	mid.x += cos(angle) * len;
	mid.y += sin(angle) * len;
	int ret = 0;
	for (int i = 0; i < n; i ++){
		if (dis_pp(mid,p[i]) <= 1 + EPS) ++ret;
	}
	return ret;
}

int main(){ 
	while (~scanf("%d",&n) && n){
		for (int i = 0; i < n; i ++){
			scanf("%lf%lf", &p[i].x, &p[i].y);
		}
		sort(p, p + n, cmp);
		int ans = 1;
		for (int i = 0; i < n; i ++){
			for (int j = i + 1; j < n && (p[j].x - p[i].x <= 2); j ++){
				if (dis_pp(p[i],p[j]) <= 4 + EPS){
					ans = max(ans, max(solve(p[i],p[j]),solve(p[j],p[i])));
				}
			}
		}
		printf("%dn",ans);
	}
	return 0;
}

还有一个O(n^2 log n)的算法，这种方法其实也简单，先枚举一个点，再枚举所有与它距离小于2的点（保证两圆相交），这样就可以求出相交弧，对于每一个圆把所有弧保存下来（只保存弧上的那两个端点一个设为-1一个设为1），并离散化（把端点存到数组里面，然后按照极角排序），这样从极角最小的开始扫，直到扫到端点对数达到这个圆上的弧的个数为止，每次扫描从1开始，标记这个弧开始了sum++，然后直到扫到这个弧结束扫到-1，这时sum—，相当于区间最大和。

就能算出覆盖次数最多的一段弧，这个次数也就是答案了，具体看代码吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151

/* From: Lich_Amnesia
 * Time: 2014-02-24 08:56:31
 *
 * POJ 1981 & ZOJ 2167
 * */
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;

const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl
#define maxn 310
#define EPS 1e-8
typedef struct Point{
	double x,y;
	Point(double x = 0, double y = 0):x(x),y(y){}
}Vector;
int n;
struct Circle{
	Point c;
	double r;
	Circle(Point c = Point(), double r = 0):c(c),r(r){}
};
struct Node{
	double angle;
	int id,flag;
}node[maxn];

bool cmp(Node a,Node b){
	return a.angle == b.angle ? a.flag > b.flag : a.angle < b.angle;
}

Vector operator + (Vector a, Vector b) {
	return Vector(a.x + b.x, a.y + b.y);
}
Vector operator - (Vector a, Vector b) {
	return Vector(a.x - b.x, a.y - b.y);
}
Vector operator * (Vector a, double k) {
	return Vector(a.x * k, a.y * k);
}

inline double cross(Vector a, Vector b) {
	return a.x * b.y - a.y * b.x;
}
inline double dis_pp(Point a,Point b){
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

Point intersection_ll(Point a, Vector i, Point b, Vector j) {
	Vector k = a - b;
	double t = cross(j, k) / cross(i, j);
	return a + i * t;
}

// 计算直线与圆的交点保证直线与圆有交点,
// 计算线段与圆的交点可用这个函数后判点是否在线段上
void intersection_cl(Circle c, Point p, Vector v, Point &p1 , Point &p2) {
	Point l1 = p, l2 = p + v;
	Vector u = Vector(-v.y, v.x);
	Point p0 = intersection_ll(p, v, c.c, u);
	double d1 = dis_pp(p0 , c.c);
	double d2 = dis_pp(l1 , l2);
	double t = sqrt(c.r * c.r - d1 * d1)/ d2;
	p1.x = p0.x + (l2.x - l1.x) * t;
	p1.y = p0.y + (l2.y - l1.y) * t;
	p2.x = p0.x - (l2.x - l1.x) * t;
	p2.y = p0.y - (l2.y - l1.y) * t;
}

// pre -req: 保证圆与圆有交点, 圆心不重合
void intersection_cc(Circle c1 , Circle c2 , Point& p1 , Point& p2){
	double d = dis_pp(c1.c, c2.c);
	double t = (1.0 + (c1.r * c1.r - c2.r * c2.r) / d / d) / 2;
	Point u = Point(c1.c.x + (c2.c.x - c1.c.x) * t, c1.c.y + (c2.c.y - c1.c.y) * t);
	Point v = Point(u.x + c1.c.y - c2.c.y, u.y - c1.c.x + c2.c.x);
	intersection_cl(c1 , u, v - u, p1 , p2);
}

Point p[maxn];

inline int solve(int n){
	int ret = 1,cnt = 0;
	bool vis[maxn];
	for (int i = 0; i < n; i ++){
		cnt = 0;
		for (int j = 0; j < n; j ++){
			if (i == j) continue;
			if (dis_pp(p[i], p[j]) > 2 + EPS) continue; //也许不需要开根
			Point a,b;
			intersection_cc(Circle(p[i],1), Circle(p[j],1), a, b);
			node[cnt].id = j;
			node[cnt].flag = -1;
			node[cnt ++].angle = atan2(a.y - p[i].y, a.x - p[i].x);

			node[cnt].id = j;
			node[cnt].flag = 1;
			node[cnt ++].angle = atan2(b.y - p[i].y, b.x - p[i].x);
		}

		if (cnt == 0) continue;

		sort(node, node + cnt, cmp);
		memset(vis,0,sizeof(vis));

		int s = 0,sum = 1,k = 0;//s表示弧的对数
		while (s < cnt / 2){
			if (node[k].flag > 0){
				sum ++;
				ret = max(ret,sum);
				vis[node[k].id] = 1; // 标记进入
			}else {
				if (vis[node[k].id]){//遇到出去的点，并且之前已经进去过，
									//那么走过了一个完整的弧，标记下
					s ++;
					sum --;
				}
			}
			k ++;//保持k在0 到cnt-1
			k %= cnt;

		}

	}
	return ret;
}

int main(){ 
	while (~scanf("%d",&n) && n){
		for (int i = 0; i < n; i ++){
			scanf("%lf%lf", &p[i].x, &p[i].y);
		}

		printf("%dn",solve(n));
	}
	return 0;
}

Posted on Edited on

这个问题最初表述为：

你有一个天平秤和12个硬币，其中1个是假的。假冒重量比其他硬币少或者多。你能确定假币是哪一枚，并判断它是重还是轻？

较难并且较为普遍的问题是：

对于一些给定的n>1，有（3^ N - 3）/2个硬币，其中1是假冒的。假冒重量比其他硬币少或者多。你能用天平秤，确定伪造硬币，并判断它是重还是轻？

The solution for 3 coins

对于 n = 2, 总共3个硬币,称重步骤如下:

1 against 2
1 against 3

对于每一次称重都有三种结果：倾向left(l)，倾向right(r)，或者balance(b)。如下表格给出了对于每种结果的答案:

l l     1 too heavy
l b     2 too light
l r     (not possible)
b l     3 too light
b b     no fake coin
b r     3 too heavy
r l     (not possible)
r b     2 too heavy
r r     1 too light

其中 l r 以及 r l 是永远不会出现的结果。

The solution for 12 coins

现在，对于n = 3,我们替换原先一个硬币c换成3c-2,3c-1以及3c。按照上面所说的方法:

1 2 3  against  4 5 6
1 2 3  against  7 8 9

这样两次之后，我们就知道哪一个集合({1,2,3}, {4,5,6} ,{7,8,9})里面有那个假冒的硬币，并且可以知道假冒的硬币是重了还是轻了。再通过一次称重操作，我们就可以确定哪一个是假冒的硬币，只要每一个集合取一个放在左边，每一个集合取一个放在右边:

   1 4 7  against  2 5 8

但是这样只能解出1到9的结果，总共有12 (= (3^3 - 3)/2)个。考虑到结果集合里不会出现 “l r” 以及”r l”(上面的两个123的称重方法)。可以利用这个条件，把10，11, 12，放进式子里:

1 2 3 10  against  4 5 6 11
1 2 3 11  against  7 8 9 10
1 4 7 10  against  2 5 8 12

这样如果不是如下情况的话，假冒的就是在1-9，否则就是在10-12里面的。根据结果分析得出:

l r l       10 too heavy
l r b       11 too light
l r r     (not possible)
b b l       12 too light
b b b       no fake coin
b b r       12 too heavy
r l l     (not possible)
r l b       11 too heavy
r l r       10 too light

Intermezzo

另外的一种解决的方案:

   1 4 6 10  against  5 7 9 12
   2 5 4 11  against  6 8 7 10
   3 6 5 12  against  4 9 8 11

对于这个方案，”l l l”与”r r r”并不可能。

可以考虑这个问题，有多少不同方案？可以确定假冒的硬币，并且确定是重了还是轻了

The solution for 39 (and more) coins

现在我们可以考虑一下如何解决n = 4的情况。同理，我们替换原先一个硬币c换成3c-2,3c-1以及3c。这样可以解决36的硬币，现在还差3个。现在我们还是按照上面的两种结果是不可能的”l r r”与”r l l”，于是我们又按照上次的方法来加入三个硬币:

 ........... 37  against ........... 38
 ........... 38  against ........... 37
 ........... 38  against ........... 37
 1 4 7 .. 34 38  against 2 5 8 .. 35 39

如此推断，对于任意的n > 1，我们都能用n次称重找到那个假冒的硬币。

Posted on Edited on

在TED上看到他StephenWolfram的一个演讲，有关A new kind of science,通过对所有知识的计算来分析出一定的结论。根据已知知识来推算未知部分，是人工智能的一部分，但是一般所能想到的比如根据已知蛋白质序列推出未知序列的结构。

但是他所想的却不一样，在计算空间之下，利用简单的规则组合成复杂形式，探讨我们这个物理世界的本质。或者是通过简单音符的组合来进行歌曲的创作。

现在已经做出来的[http://www.wolframalpha.com/](http://www.wolframalpha.com/)已经可以做到进行实时的知识检索以及分析了，实在是太nice了。把所有已知知识进行汇总计算，推导出来的是不是就是原来未知的东西，那岂不是就可以探寻本质了么？非常佩服~

有关wolfram alpha 请戳:[http://zh.wikipedia.org/wiki/Wolfram_Alpha](http://zh.wikipedia.org/wiki/Wolfram_Alpha)

还有在这之前建立的数学检索库: [http://mathworld.wolfram.com/](http://mathworld.wolfram.com/)



以下附上那篇TED演讲以及有关论文

链接：[http://pan.baidu.com/s/1dDtGGM1](http://pan.baidu.com/s/1dDtGGM1) 密码：ip16

Posted on Edited on

在使用Word办公时，我们经常需要批量查找替换，但是直接进行文字替换时，经常是达不到我们期望的效果，这时我们就需要增加一些通配符来查找了。下面给大家列出Word查找/替换栏代码·通配符一览表，具体的实例我们将在以后的文章中陆续介绍。例如，Word查找替换总是反引号，怎么办？

Word 查找栏代码&middot;通配符一览表
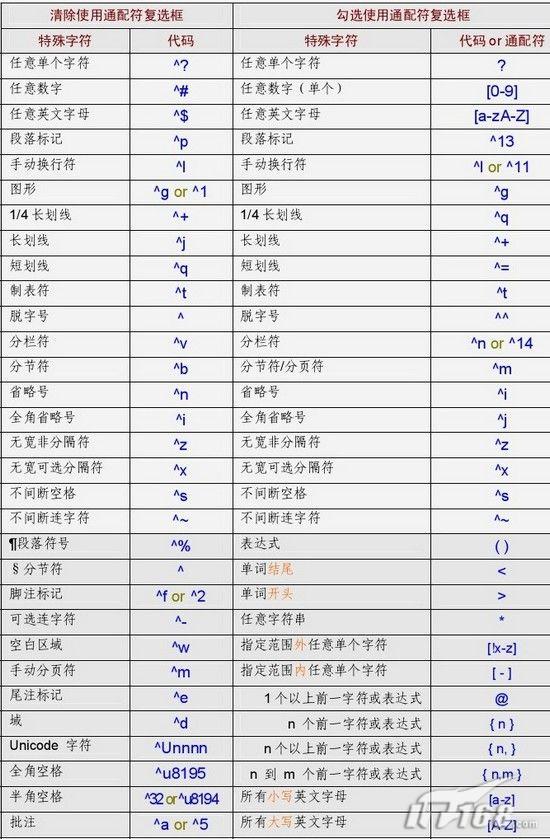![Word查找替换栏代码和通配符一览表](http://i1.sinaimg.cn/IT/s/s/2008-03-06/f6ed2d9533a7632424373f84ef3fbfd8.jpg)
图1 通配符
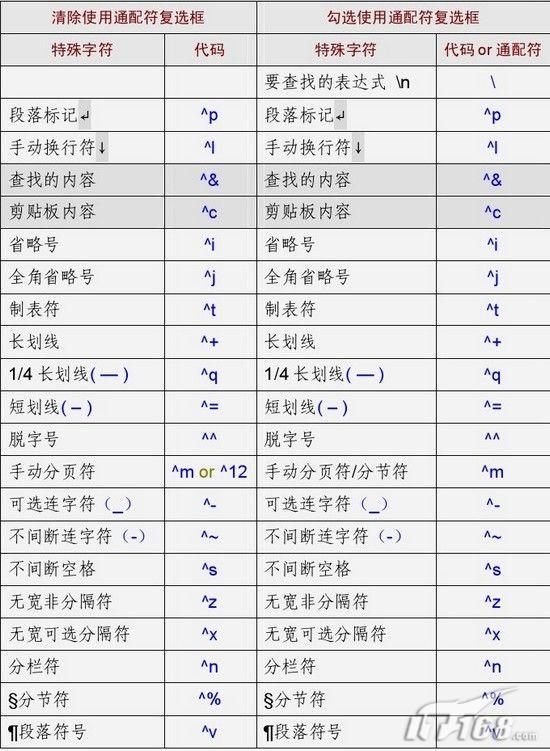![Word查找替换栏代码和通配符一览表](http://i2.sinaimg.cn/IT/s/s/2008-03-06/91e65ea770fbc8a22459852a658e9ae9.jpg)
图2 通配符 
　　注：要查找已被定义为通配符的字符，该字符前键入反斜杠  。查找？、*、（、）、[ 、] 等的代码分别是？、*、(、)、[、] 。