本文介绍机器学习基本的数学知识、常用函数。以及介绍了梯度下降算法。

虽然之前已经看过一遍这本书，但一直没有留下笔记，很多东西又有遗忘，所以记下一下重要的东西。

Windows配置VPN，选择“使用IPsec的第2层隧道协议(L2TP/IPSec)”时，有时候正常有时候。

1. 单击“开始”，单击“运行”，键入“regedit”，然后单击“确定”

2. 找到下面的注册表子项，然后单击它： HKEY_LOCAL_MACHINE\ System\CurrentControlSet\Services\Rasman\Parameters

3. 在“编辑”菜单上，单击“新建”->“DWORD值”

4. 在“名称”框中，键入“ProhibitIpSec”

5. 在“数值数据”框中，键入“1”，然后单击“确定”

6. 退出注册表编辑器，然后重新启动计算机

因为我们是朋友，所以你可以使用我的文字，但请注明出处：http://alwa.info

本文主要介绍了RBM(受限制玻尔兹曼机)。首先介绍背景知识，然后介绍了RBM的结构。最后讲了一下它为什么是一种DL方法，引出DBN。

本文主要讲Theano的安装，以及Theano的基本操作。最后给了一个完整的logistics回归的例子。

本文介绍了如何使用shell_plus进行本机Judge的Model调试

1. CNN 介绍

卷积神经网络是人工神经网络的一种，已成为当前语音分析和图像识别领域的研究热点。它的权值共享网络结构使之更类似于生物神经网络，降低了网络模型的复杂度，减少了权值的数量。该优点在网络的输入是多维图像时表现的更为明显，使图像可以直接作为网络的输入，避免了传统识别算法中复杂的特征提取和数据重建过程。卷积网络是为识别二维形状而特殊设计的一个多层感知器，这种网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。

CNNs是第一个真正成功训练多层网络结构的学习算法。它利用空间关系减少需要学习的参数数目以提高一般前向BP算法的训练性能。在CNN中，图像的一小部分（局部感受区域）作为层级结构的最低层的输入，信息再依次传输到不同的层，每层通过一个数字滤波器去获得观测数据的最显著的特征。这个方法能够获取对平移、缩放和旋转不变的观测数据的显著特征，因为图像的局部感受区域允许神经元或者处理单元可以访问到最基础的特征，例如定向边缘或者角点。

这部片子算是之前给我印象比较深刻的布达佩斯大饭店之后觉得非常值得看的一部片子了。

1. 卷积特征

1.1 全联通网络

　　全联通网络就是指输入层和隐含层进行全链接的设计。实际计算角度来讲，会出现很大的图像比如（96x96）大小的。那么计算上就会非常消耗时间，因为有$10^4$的计算输入单元，并且如果需要训练出100个特征，那么就会有$10^6$次方个参数需要学习。 　　

1.2 部分联通网络

　　上面的简单的解决策略就是设计对隐含单元和输入单元间连接的限制。每个隐含单元只能是输入单元的一部分。 　　

1.3 卷积　　

　　卷积是自然图像的固有属性，意思就是从一个大尺寸的图像中随机选取一块，比如8x8的作为样本，并且从这个小样本中学习到了一些特征。把这些特征作为探测器来应用到大图像的任意地方去。可以使用8x8的样本学习到的特征跟原本的大尺寸图像做卷积，从而对这个大尺寸图像的任意位置获得一个不同特征的激活值。
　　
　　假设给定了$ r \times c $ 的大尺寸图像，将其定义为 $x_{large}$。首先通过从大尺寸图像中抽取的 $a \times b $的小尺寸图像样本 $x_{small}$ 训练稀疏自编码，计算$ f = σ(W^{(1)}_{xsmall} + b(1))$（σ 是一个 sigmoid 型函数）得到了 k 个特征， 其中$ W^{(1)} $和$ b^{(1)} $是可视层单元和隐含单元之间的权重和偏差值。对于每一个$ a \times b $大小的小图像 $x_s$，计算出对应的值$ f_s = σ(W^{(1)}x_s + b^{(1)})$，对这些 $f_{convolved}$ 值做卷积，就可以得到$ k \times (r - a + 1) \times (c - b + 1) $个卷积后的特征的矩阵。

1. 使用自我学习到深层网络模型

　　在自我学习中，我们首先利用未标注数据训练一个稀疏自编码器。随后，给定一个新样 x，我们通过隐含层提取出特征 a。如下所示

　　我们感兴趣的是分类问题，目标是预测样本的类别标号 y。我们拥有标注数据集 $\{ (x_l^{(1)}, y^{(1)}), (x_l^{(2)}, y^{(2)}), \ldots (x_l^{(m_l)},y^{(m_l)}) \} ，包含 $m_l$ 个标注样本。此前我们已经说明，可以利用稀疏自编码器获得的特征 $a^{(l)} 来替代原始特征。这样就可获得训练数据集 $ \{ (a^{(1)},y^{(1)}), \ldots (a^{(m_{l})}, y^{(m_l)}) \} $。最终，我们训练出一个从特征 $a^{(i)}$ 到类标号 $y^{(i)}$ 的 logistic 分类器。为说明这一过程，我们按照神经网络一节中的方式，用下图描述 logistic 回归单元（橘黄色）。

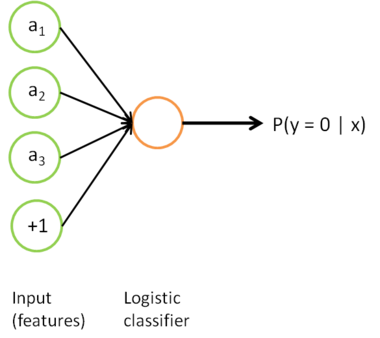
　　考虑利用这个方法所学到的分类器（输入-输出映射）。它描述了一个把测试样本 x 映射到预测值 $ p(y=1|x) $的函数。将此前的两张图片结合起来，就得到该函数的图形表示。最终的分类器就是：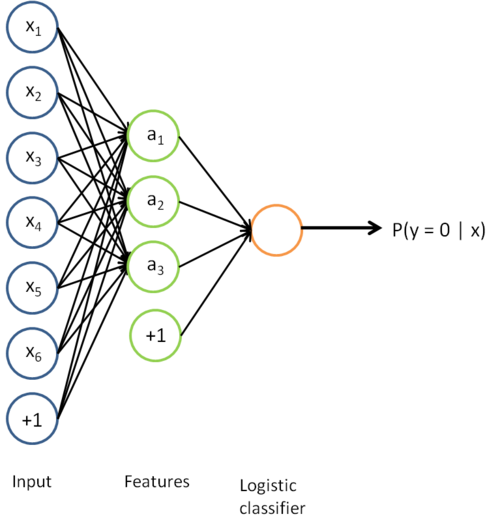

　　该模型的参数通过两个步骤训练获得：在该网络的第一层，将输入 x 映射至隐藏单元激活量 a 的权值$ W^{(1)} $可以通过稀疏自编码器训练过程获得。在第二层，将隐藏单元 a 映射至输出 y 的权值$ W^{(2)} $可以通过 logistic 回归或 softmax 回归训练获得。

　　这个最终分类器整体上显然是一个大的神经网络。因此，在训练获得模型最初参数（利用自动编码器训练第一层，利用 logistic/softmax 回归训练第二层）之后，我们可以进一步修正模型参数，进而降低训练误差。具体来说，我们可以对参数进行微调，在现有参数的基础上采用梯度下降或者 L-BFGS 来降低已标注样本集$ \{ (x_l^{(1)}, y^{(1)}), (x_l^{(2)}, y^{(2)}), \ldots (x_l^{(m_l)}, y^{(m_l)}) \} $上的训练误差。

　　使用微调时，初始的非监督特征学习步骤（也就是自动编码器和logistic分类器训练）有时候被称为预训练。微调的作用在于，已标注数据集也可以用来修正权值$ W^{(1)}$，这样可以对隐藏单元所提取的特征 a 做进一步调整。

　　目前我们使用的都是“替代”，并没有使用“级联”。替代中，logistics分类器所看到的训练样本格式为 $ (a^{(i)}, y^{(i)})$；而在级联表示中，分类器所看到的训练样本格式为 $ ((x^{(i)}, a^{(i)}), y^{(i)})$。

一般如果要进行微调的时候，采用替代，因为级联慢。而且通常是有大量已标注训练数据的情况下。微调能显著提升分类器性能。然而只有相对较少的已标注训练集，微调的作用就很有限了。