统计学习方法笔记(一) 监督学习基础知识

虽然之前已经看过一遍这本书，但一直没有留下笔记，很多东西又有遗忘，所以记下一下重要的东西。

1. 监督学习一些定义

1.1 输入空间、特征空间与输出空间

在监督学习中，将输入与输出所有可能的取值集合称为输入空间和输出空间。每个输入是一个实例，通常用特征向量表示。所有特征向量存在的空间称为特征空间。
Feature Vector: $x = (x^{(1)},x^{(2)},\dots,x^{(i)},\dots,x^{(n)})^T$。其中$x^{(i)}$表示第i个特征。通常用$x_i$表示多个输入变量的第i个。表示为：

$$x\_i = (x\_i^{(1)},x\_i^{(2)},\dots,x\_i^{(n)})^T$$

训练数据由输入与输出成对组成，表示成：

$$T = \\{(x\_1,y\_1),(x\_2,y\_2),\dots,(x\_N,y\_N)\\}$$

测试数据也由相应的输入和输出成对组成。输入与输出又称为样本（sample）。

1.2 联合概率分布

监督学习假设输入和输出随机变量X和Y遵循联合概率分布P(X,Y)。如下定义：

$$P(X = x\ and\ Y = y) = P(Y = y | X = x) * P(X = x)$$

1.3 问题形式化

学习模型是属于输入空间到输出空间的映射的集合。这个集合就是假设空间（hypothesis space）。
监督学习的模型可以是概率模型或者非概率模型。由条件概率分布$P(Y|X)$或者决策函数$Y=f(X)$表示。
监督学习可以分为学习和预测两个过程，由学习系统与预测系统完成。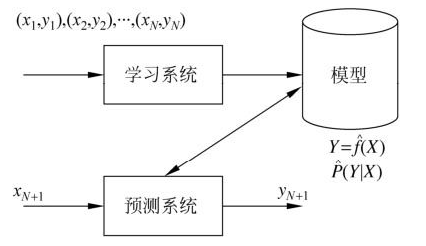

2. 统计学习方法三要素

2.1 模型

模型主要分为条件概率分布和决策函数。
假设空间设为$\digamma$，可以设为决策函数的集合或者条件概率的集合。

$$\begin{align} & \text{决策函数集合: } \digamma = \\{f | Y = f(X)\\} \\\\ & \text{条件概率集合: } \digamma = \\{P | P(Y | X)\\} \end{align}$$

2.2 策略

2.2.1 损失函数与风险函数

有了模型的假设空间，现在需要一个评判标准来学习或者选择最优模型。统计学习的目标在于在假设空间中选取最优模型。
监督学习在假设空间中选取了f作为决策函数，那么对于给定输入X，由f(X)得到相应输出Y，但是这个预测值f(X)与真实值Y还是可能不一样的，用损失函数（loss function）或者代价函数（cost function）来度量预测错误的程度。记作$L(Y,f(X))$
常用的损失函数有以下几种：
(1) 0-1损失函数：

$$L(Y,f(x)) = \left\\{ \begin{aligned} 1 , Y \ne f(X) \\\\ 0 , Y = f(X) \end{aligned} \right.$$

(2) 平方损失函数：

$$L(Y,f(x)) = (Y - f(X))^2$$

(3) 绝对损失函数：

$$L(Y,f(x)) = |Y - f(X)|$$

(4) 对数损失函数：

$$L(Y,P(Y|X)) = -logP(Y|X)$$

关于模型的平均损失称为经验风险，或者经验损失，记作$R_{emp}$：

$$R\_{emp}(f) = \frac{1}{N}\sum\_{i=1}^{N}L(y\_i,f(x\_i))$$

期望风险$R_{exp}(f)$是模型关于联合分布的期望损失，经验风险$R_{emp}$是模型关于训练样本集的平均损失。当样本N趋向于无穷时，经验风险趋于期望风险。所以很自然的使用经验风险估计期望风险。但实际上是需要进行一定矫正的，有两个基本策略：经验风险最小化和结构风险最小化。

2.2.2 经验风险最小化与结构风险

经验风险最小化（ERM）的策略认维，经验风险最小的模型就是最优的模型。求解最优化问题：

$$\min\_{f \in \digamma} \frac{1}{N} \sum\_{i=1}^{N}L(y\_i,f(x\_i))$$

其中F是假设空间。当样本空间足够大的时候经验风险最小化保证有很好的学习效果。比如极大似然估计就是很好的例子。当模型是条件概率分布事，损失函数是对数损失函数，等价于极大似然估计。
注意：当样本很小的时候，经验风险容易导致过拟合问题。

结构风险最小化（SRM）是为了防止过拟合提出来的。等价于正则化。结构风险在经验风险上加上表示模型复杂度的正则化项或者罚项。结构风险定义是

$$R\_{srm}(f) = \frac{1}{N} \sum\_{i=1}^{N}L(y\_i,f(x\_i)) + \lambda J(f)$$

其中$J(f)$表示的模型的复杂度。$\lambda$是系数，权衡经验风险和模型复杂度。模型f越复杂，复杂度$J(f)$就越大，反之亦然。
比如，贝叶斯估计中的最大后延概率估计（MAP）就是结构风险最小化的一个例子。
求解最优模型就是求解最优化问题：

$$\min\_{f \in \digamma} \frac{1}{N} \sum\_{i=1}^{N}L(y\_i,f(x\_i)) + \lambda J(f)$$

2.3 算法

算法是指学习模型的具体计算方法。这个时候，统计学习问题已经归结为最优化问题。但是这个最优化问题基本没有解析解需要通过数值方法进行求解。

3. 模型评估

3.1 测试误差

3.2 归一化和正则化

4. 生成模型和判别模型

监督学习又可以分为生成方法和判别方法。所得到模型又叫生成模型和判别模型。
生成方法由数据学习联合概率分布P(X,Y)然后求P(Y|X)作为预测模型，即生成模型：

$$P(Y|X) = \frac{P(X,Y)}{P(X)}$$

叫做生成方法，是因为模型表示了给定输入X产生输入Y的生成关系。典型的有：朴素贝叶斯和隐马尔科夫模型。
生成方法特点：可以还原联合概率分布P(X,Y)。收敛速度更快
判别方法由数据直接学习决策函数f(x)或者条件概率分布P(Y|X)作为预测模型。关系的是给定输入的X，预测什么样的输出Y。典型的有：k近邻、感知机、决策树、逻辑斯蒂回归模型、最大熵模型、支持向量机等。
判别方法特点：直接学习决策函数f(x)或者条件概率分布P(Y|X)，学习准确率更好。而且直接学习可以对数据进行抽象、定义特征使用特征，可以简化学习问题。

---

　

因为我们是朋友，所以你可以使用我的文字，但请注明出处：http://alwa.info