本文介绍机器学习基本的数学知识、常用函数。以及介绍了梯度下降算法。

1. 数学基础

1.1 向量范数

　　范数(norm)是一个表示长度的函数。对一个n维的向量X，常见范数有：
　　L1范数： $|X|\_1 = \sum\_{i=1}^{n}|x\_i|$
　　L2范数： $||X||\_2 = \sqrt{\sum\_{i=1}^{n}x\_i^2} = \sqrt{X^TX}$

1.2 矩阵偏导数

　　参考这篇博文：http://blog.sina.com.cn/s/blog_4a033b090100pwjq.html

1.3 常用函数

　　logistic函数：经常用来将一个实数空间映射到(0,1)区间，记为$\sigma(x)$

$\sigma(x) = \frac{1}{1 + e^{-x}}$

　　导数为：

$\sigma'(x) = \sigma(x)(1 - \sigma(x))$

softmax函数：将多个标量映射为一个概率分布
　　后面的文章会进行介绍

　　假设我们给出一个损失函数，这是一个平方损失。

$J(θ) = \frac{1}{2} \sum\_i^{n}{||h\_θ(x\_i) - y\_i||^2}$

　　使这个式子最小。有一些参数学习算法可以求解。这样求解的过程称之为训练过程。下面来介绍一下常用的参数学习算法：梯度下降法

2. 梯度下降法

2.1 迭代公式介绍

　　梯度下降法的迭代公式为：

$a\_{t+1} = a\_{t} - \lambda\nabla f(a\_t)$

　　其中$\lambda > 0$是梯度方向上的搜索步长。
　　我们可以从一个初值$x_0$开始，通过迭代公式得到$x_1,x_2,\dots,x_n$，并且满足：

$f(x\_0) \geq f(x\_1) \geq \dots \geq f(x\_n)$

　　最终能够收敛到$x_n$，为最终的极值。
　　在机器学习问题中，我们需要学习参数$\theta$使得风险函数最小化。也就是

$\begin{align} \theta^\* &= \arg\min\_{\theta}R(\theta\_t) \\\\ &= \arg\min\_{\theta}\frac{1}{N}\sum\_{i=1}^{N}L(y^{(i)},f(x^{(i)},\theta) \end{align}$

　　$\arg\min$的意思就是：表示使目标函数取最小值时的变量值

$\underset{x}{\operatorname{arg\,max}} \, f(x) := \\{x\\ |\\ \forall y : f(y) \le f(x)\\}$

　　如果使用梯度下降进行参数学习，则：

$\begin{align} a\_{t+1} &= a\_t - \lambda \frac{\partial R(\theta)}{\partial \theta\_t} \\\\ &= a\_t - \lambda \sum\_{i=1}^{N}\frac{\partial R(\theta;x^{(i)},y^{(i)})}{\partial \theta} \end{align}$

　　这里梯度下降求解所有样本函数最小值，叫做批量梯度下降。
　　但是如果样本N或者X维数很大的时候，批量梯度下降效率低，引入一个改进随机梯度下降法(SGD)。每个样本都进行更新，表示为：

$a\_{t+1} = a\_t - \lambda \frac{\partial R(\theta;x^{(i)},y^{(i)})}{\partial \theta}$

2.2 梯度下降的过程

　　梯度下降法是按下面的流程进行的：
　　1）首先对$\theta$赋值，这个值可以是随机的，也可以让$\theta$是一个全零的向量。
　　2）改变$\theta$的值，使得$J(θ)$按梯度下降的方向进行减少。

　　为了更清楚，给出下面的图：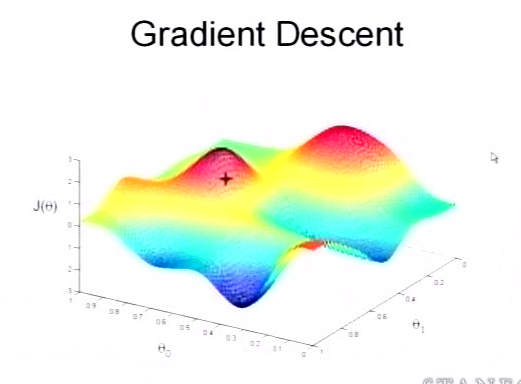

　　这是一个表示参数$θ$与误差函数$J(θ)$的关系图，红色的部分是表示$J(θ)$有着比较高的取值，我们需要的是，能够让$J(θ)$的值尽量的低。也就是深蓝色的部分。$θ_0$，$θ_1$表示$θ$向量的两个维度。
　　在上面提到梯度下降法的第一步是给$θ$给一个初值，假设随机给的初值是在图上的十字点。
　　然后我们将$θ$按照梯度下降的方向进行调整，就会使得$J(θ)$往更低的方向进行变化，如图所示，算法的结束将是在$θ$下降到无法继续下降为止。
　　

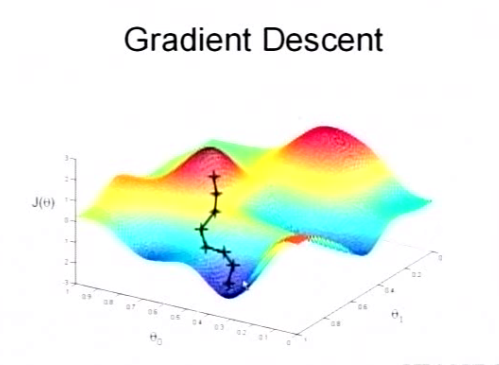
　　当然，可能梯度下降的最终点并非是全局最小点，可能是一个局部最小点，可能是下面的情况：

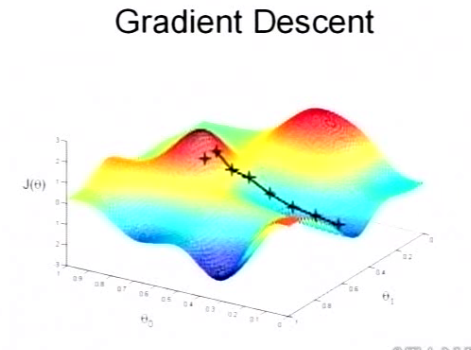
　　上面这张图就是描述的一个局部最小点，这是我们重新选择了一个初始点得到的，看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点。

2.3 学习速率设置

　　在梯度下降学习过程中，学习率的取值非常关键，如果过大就不会收敛，过小则收敛速度特别慢。所以机器学习中使用自适应调整学习率的方法。

2.3.1 动量法

　　就是在迭代过程中加入上一次迭代的更新。记作$\nabla \theta_t = \theta_t - \theta_{t-1}$。在第t次迭代的时候。

$\theta\_t = \theta\_{t-1} + (\rho\nabla\theta\_{t} - \lambda g\_t)$

　　其中$\rho$为动量因子，经常设置为0.9。迭代初期相同方向加速，迭代后期方向相反，增加稳定性。

2.3.2 AdaGrad

2.3.3 AdaDelta

2.4 梯度下降缺点

靠近极小值时速度减慢。
直线搜索可能会产生一些问题。
可能会’之字型’地下降。

因为我们是朋友，所以你可以使用我的文字，但请注明出处：http://alwa.info

Shen Huang's Blog

机器学习基础知识和梯度下降算法介绍