1. 综述
如果已经有一个足够强大的机器学习算法,为了获得更好的性能,最靠谱的方法之一是给这个算法以更多的数据。机器学习界甚至有个说法:“有时候胜出者并非有最好的算法,而是有更多的数据。”
但是现实中,人们已经花了很多精力进行手工标数据。如果算法能够从未标注数据中学习,那么我们就可以轻易地获取大量无标注数据,并从中学习。自学习和无监督特征学习就是这种的算法。尽管一个单一的未标注样本蕴含的信息比一个已标注的样本要少,但是如果能获取大量无标注数据(比如从互联网上下载随机的、无标注的图像、音频剪辑或者是文本),并且算法能够有效的利用它们,那么相比大规模的手工构建特征和标数据,算法将会取得更好的性能。
在自学习和无监督特征学习问题上,可以给算法以大量的未标注数据,学习出较好的特征描述。在尝试解决一个具体的分类问题时,可以基于这些学习出的特征描述和任意的(可能比较少的)已标注数据,使用有监督学习方法完成分类。
2. 自编码神经网络
2.1 自编码神经网络含义
在有监督学习中,训练样本是有类别标签的。现在假设我们只有一个没有带类别标签的训练样本集合 $ \{x^{(1)}, x^{(2)}, x^{(3)}, \ldots\} $,其中 $ x^{(i)} \in \Re^{n}$ 。自编码神经网络是一种无监督学习算法,它使用了反向传播算法,并让目标值等于输入值,比如 $ y^{(i)} = x^{(i)} $。下图是一个自编码神经网络的示例。
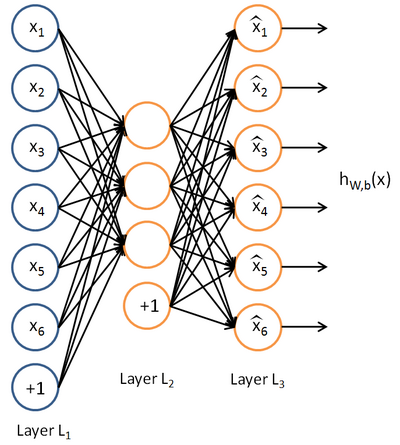
自编码神经网络是尝试学习一个$ h_{W,b}(x) \approx x $ 函数。也就是说它尝试逼近一个恒等函数,使得输出$ \hat{x} $接近于输入$x $。恒等函数虽然看上去没有学习的意义,但是当我们为自编码神经网络加入某些限制,比如限制隐藏神经元的数量,可以发现从输入数据发现一个有意义的结构。
比如说神经网络的输入是一个10*10的图像,这样维度就是100,输出层也是$ y \in \Re^{100}$。但是网络中只有50个隐藏神经元,这个就让网络能够学习输入数据压缩表示。有的时候如果输入每一维都是独立同分布的高斯随机变量,那么压缩会非常难学习,但是如果某些输入特征是彼此相关的,那么这一算法就可以发现输入数据的这些相关性。
这个有点类似于主成分分析(PCA)的输入数据的低维表示。
2.2 稀疏性限制
上面是隐藏神经元比较少的时候的假设。如果说隐藏神经元很多(比输入还多)。可以给一些其他限制发现输入数据的结构。
稀疏性可以被简单地解释如下。如果当神经元的输出接近于1的时候我们认为它被激活,而输出接近于0的时候认为它被抑制,那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。这里我们假设的神经元的激活函数是sigmoid函数。如果你使用tanh作为激活函数的话,当神经元输出为-1的时候,我们认为神经元是被抑制的。
注意到 $ a^{(2)}_j $表示隐藏神经元 j 的激活度,但是这一表示方法中并未明确指出哪一个输入 x 带来了这一激活度。所以我们将使用$ a^{(2)}_j(x) $来表示在给定输入为 x 情况下,自编码神经网络隐藏神经元 j 的激活度。 进一步,使用
表示隐藏神经元 j 的平均活跃度(在训练集上取平均)。我们可以近似的加入一条限制
其中, $ \rho $是稀疏性参数,通常是一个接近于0的较小的值(比如 $ \rho = 0.05$ )。换句话说,我们想要让隐藏神经元j的平均活跃度接近0.05。为了满足这一条件,隐藏神经元的活跃度必须接近于0。
为了实现这一限制,我们将会在我们的优化目标函数中加入一个额外的惩罚因子,而这一惩罚因子将惩罚那些 $ \hat\rho_j $和$\rho$有显著不同的情况从而使得隐藏神经元的平均活跃度保持在较小范围内。惩罚因子的具体形式有很多种合理的选择,我们将会选择以下这一种:
\begin{align}
\sum_{j=1}^{s_2} \rho \log \frac{\rho}{\hat\rho_j} + (1-\rho) \log \frac{1-\rho}{1-\hat\rho_j}.
\end{align}
这里, $ s_2$ 是隐藏层中隐藏神经元的数量,而索引 j 依次代表隐藏层中的每一个神经元。如果你对相对熵(KL divergence)比较熟悉,这一惩罚因子实际上是基于它的。于是惩罚因子也可以被表示为:
其中 $ {\rm KL}(\rho || \hat\rho_j)
= \rho \log \frac{\rho}{\hat\rho_j} + (1-\rho) \log \frac{1-\rho}{1-\hat\rho_j} $是一个以 $ \rho $为均值和一个以 $ \hat\rho_j$ 为均值的两个伯努利随机变量之间的相对熵。相对熵是一种标准的用来测量两个分布之间差异的方法。
这一惩罚因子有如下性质,当$ \hat\rho_j = \rho $时 ${\rm KL}(\rho || \hat\rho_j) = 0 $,并且随着 $ \hat\rho_j $与 $ \rho$ 之间的差异增大而单调递增。
现在,我们的总体代价函数可以表示为:
其中 $ J(W,b) $如之前所定义,而 $ \beta$ 控制稀疏性惩罚因子的权重。 $ \hat\rho_j $项则也(间接地)取决于 $ W,b$ ,因为它是隐藏神经元 j 的平均激活度,而隐藏层神经元的激活度取决于 $ W,b $。
为了对相对熵进行导数计算,我们可以使用一个易于实现的技巧。
具体来说,前面在后向传播算法中计算第二层( $ l=2 $)更新的时候我们已经计算了
\begin{align}
\delta^{(2)}_i = \left( \sum_{j=1}^{s_{2}} W^{(2)}_{ji} \delta^{(3)}_j \right) f’(z^{(2)}_i),
\end{align}
现在我们将其换成
\begin{align}
\delta^{(2)}_i = \left( \left( \sum_{j=1}^{s_{2}} W^{(2)}_{ji} \delta^{(3)}_j \right) + \beta \left( - \frac{\rho}{\hat\rho_i} + \frac{1-\rho}{1-\hat\rho_i} \right) \right) f’(z^{(2)}_i) .
\end{align}
就可以了。
注意:$ \hat\rho_i$ 来计算这一项更新。所以在计算任何神经元的后向传播之前,你需要对所有的训练样本计算一遍前向传播,从而获取平均激活度。
3. 自我学习
3.1 特征学习
我们已经了解到如何使用一个自编码器(autoencoder)从无标注数据中学习特征。具体来说,假定有一个无标注的训练数据集 $ \{ x_u^{(1)}, x_u^{(2)} $, \ldots, x_u^{(m_u)}\}(下标 u 代表“不带类标”)。现在用它们训练一个稀疏自编码器(可能需要首先对这些数据做白化或其它适当的预处理)。
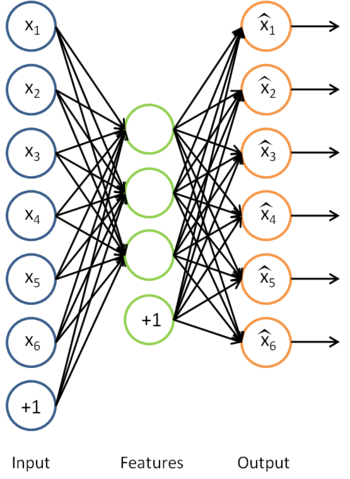
利用训练得到的模型参数 $ W^{(1)}, b^{(1)}, W^{(2)}, b^{(2)}$,给定任意的输入数据 x,可以计算隐藏单元的激活量(activations) a。如前所述,相比原始输入 x 来说, a 可能是一个更好的特征描述。下图的神经网络描述了特征(激活量 a)的计算。

这实际上就是之前得到的稀疏自编码器,在这里去掉了最后一层。
假定有大小为$ m_l $的已标注训练集$ \{ (x_l^{(1)}, y^{(1)}),
(x_l^{(2)}, y^{(2)}), \ldots (x_l^{(m_l)}, y^{(m_l)}) \}$(下标 l 表示“带类标”),我们可以为输入数据找到更好的特征描述。例如,可以将$ x_l^{(1)}$ 输入到稀疏自编码器,得到隐藏单元激活量$ a_l^{(1)}$。接下来,可以直接使用$ a_l^{(1)} $来代替原始数据$ x_l^{(1)} $(“替代表示”,Replacement Representation)。也可以合二为一,使用新的向量$ (x_l^{(1)}, a_l^{(1)})$ 来代替原始数据$ x_l^{(1)} $(“级联表示”,Concatenation Representation)。
经过变换后,训练集就变成$ \{ (a_l^{(1)}, y^{(1)}), (a_l^{(2)}, y^{(2)}), \ldots (a_l^{(m_l)}, y^{(m_l)})
\}$或者是$ \{
((x_l^{(1)}, a_l^{(1)}), y^{(1)}), ((x_l^{(2)}, a_l^{(1)}), y^{(2)}), \ldots,
((x_l^{(m_l)}, a_l^{(1)}), y^{(m_l)}) \}$(取决于使用$ a_l^{(1)} $替换$ x_l^{(1)} $还是将二者合并)。在实践中,将$ a_l^{(1)} $和$ x_l^{(1)}$ 合并通常表现的更好。但是考虑到内存和计算的成本,也可以使用替换操作。
最终,可以训练出一个有监督学习算法(例如 svm, logistic regression 等),得到一个判别函数对y 值进行预测。预测过程如下:给定一个测试样本$ x_{\rm test}$,重复之前的过程,将其送入稀疏自编码器,得到$ a_{\rm test}$。然后将$ a_{\rm test} $(或者$ (x_{\rm test}, a_{\rm test}) $)送入分类器中,得到预测值。
3.2 数据处理
在特征学习阶段,我们从未标注训练集 $ \{ x_u^{(1)}, x_u^{(2)}, \ldots, x_u^{(m_u)}\}$ 中学习,这一过程中可能计算了各种数据预处理参数。例如计算数据均值并且对数据做均值标准化(mean normalization);或者对原始数据做主成分分析(PCA),然后将原始数据表示为 $ U^Tx $(又或者使用 PCA 白化或 ZCA 白化)。这样的话,有必要将这些参数保存起来,并且在后面的训练和测试阶段使用同样的参数,以保证数据进入稀疏自编码神经网络之前经过了同样的变换。
3.3 常见无监督特征学习
有两种常见的无监督特征学习方式,区别在于你有什么样的未标注数据。自学习(self-taught learning) 是其中更为一般的、更强大的学习方式,它不要求未标注数据 $ x_u$ 和已标注数据 $ x_l$ 来自同样的分布。另外一种带限制性的方式也被称为半监督学习,它要求 $ x_u$和$ x_l$ 服从同样的分布。下面通过例子解释二者的区别。
参考文献
http://ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial
因为我们是朋友,所以你可以使用我的文字,但请注明出处:http://alwa.info