1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;
const int INF = ~0u>>1;
typedef pair <int,int> P;
#define MID(x,y) ((x+y)>>1)
#define iabs(x) ((x)>0?(x):-(x))
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define pb push_back
#define mp make_pair
#define print() cout<<"--------"<<endl
double a;
double F(double x){
return sqrt(1 + 4*a*a*x*x);
}
double simpson(double a,double b){
double c = a + (b-a)/2;
return (F(a) + 4*F(c) + F(b)) * (b-a) / 6;
}
double asr(double a,double b,double eps,double A){
double c = a + (b-a)/2;
double L = simpson(a,c),R = simpson(c,b);
if (fabs(L+R-A) <= 15*eps) return L+R+(L+R-A)/15.0;
return asr(a,c,eps/2,L) + asr(c,b,eps/2,R);
}
double asr(double a,double b,double eps){
return asr(a,b,eps,simpson(a,b));
}
double solve(double w,double h){
a = 4.0 * h / (w*w);
return asr(0,w/2,1e-5)*2;
}
int main(){
int t,cas = 0;
scanf("%d", &t);
while (cas++<t){
int D,H,B,L;
scanf("%d%d%d%d", &D, &H, &B, &L);
int n = (B+D-1) / D;
double D1 = (double) B / n;
double L1 = (double) L / n;
double x = 0, y = H;
while(y-x > 1e-5){
double m = x + (y-x) / 2;
if(solve(D1,m) < L1) x = m;
else y = m;
}
if(cas > 1) puts("");
printf("Case %d:n%.2fn", cas, H - x);
}
return 0;
}
|
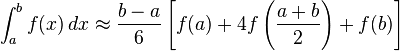 (感谢维基百科)
(感谢维基百科)